For more: https://www.echelman.com/
Theory
Michel Foucault
This is Not a Pipe
“This is Not a Pipe.”, edited by James Harkness. Quantum Books, 2008.
Original Publication: Ceci n’est pas une pipe
Excerpt – Chapter 6: Non-affirmative Painting.
Separation between linguistic signs and plastic elements; equivalence of resemblance and affirmation. These two principles constituted the tension in classical painting, because the second reintroduced discourse (affirmation exists only where there is speech) into an art from which the linguistic element was rigorously excluded. Hence the fact that classical painting spoke – and spoke constantly – while constituting itself entirely outside language; hence the fact that it rested silently in a discursive space; hence the fact that it provided, beneath itself, a kind of common ground where it could restore the bonds of signs and the image. Magritte knits verbal signs and plastic elements together, but without referring them to a prior isotopism. He skirts the base of affirmative discourse on which resemblance calmly reposes, and he brings pure similitudes and nonaffirmative verbal statements into play within the instability of a disoriented volume and an unmapped space. A process whose formulation is in some sense given by Ceci n’est pas une pipe.
- To employ a calligram where are found, simultaneously present and visible, image, text, resemblance, affirmation and their common ground.
- Then suddenly to open up, so that the calligram immediately decomposes and disappears, leaving as a trace only its own absence.
- To allow discourse to collapse of its own weight and to acquire the visible shape of letters. Letters which, insofar as they are drawn, enter into an uncertain, indefinite relation, confused with the drawing itself – but minus any area to serve as a common ground.
- To allow similitudes, on the other to multiply of themselves, to be born from their own vapour and to rise endlessly into an ether where they refer to nothing more than themselves.
- To verify clearly, at the end of the operation, that the precipitate has changed colour, that it has gone from black to white, that the “This is a pipe” silently hidden in the mimetic representation has become the “This is not a pipe” of circulating similitudes.
A day will come when, by means of similitude relayed indefinitely along the length of a series, the image itself, along with the name it bears, will lose its identity. Campbell, Campbell, Campbell.
truth
Truth is a major theme in Foucault’s work, in particular in the context of its relations with power, knowledge and the subject. He argues that truth is an event which takes place in history. It is something that ‘happens’, and is produced by various techniques (the ‘technology’ of truth) rather than something that already exists and is simply waiting to be discovered. Foucault argues that ‘the effect of truth’ he wants to produce consists in ‘showing that the real is polemical’. Foucault further notes that he is not interested in ‘telling the truth’, in his writing; rather, he is interested in inviting people to have a particular experience for themselves.
– Clare O’Farrell 2007
The Archæology of Knowledge
… These problems may be summed up in a word: the questioning of the document. Of course, it is obvious enough that ever since a discipline such as history has existed, documents have been used, questioned, and have given rise to questions; scholars have asked not only what these documents meant, but also whether they were telling the truth, and by what right they could claim to be doing so, whether they were sincere or deliberately misleading, well informed or ignorant, authentic or tampered with. But each of these questions, and all this critical concern, pointed to one and the same end: the reconstitution, on the basis of what the documents say, and sometimes merely hint at, of the past from which they emanate and which has now disappeared far behind them; the document was always treated as the language of a voice since reduced to silence, its fragile, but possibly decipherable trace. Now, through a mutation that is not of very recent origin, but which has still not come to an end, history has altered its position in relation to the document: it has taken as its primary task, not the interpretation of the document, nor the attempt to decide whether it is telling the truth or what is its expressive value, but to work on it from within and to develop it: history now organises the document, divides it up, distributes it, orders it, arranges it in levels, establishes series, distinguishes between what is relevant and what is not, discovers elements, defines unities, describes relations. The document, then, is no longer for history an inert material through which it tries to reconstitute what men have done or said, the events of which only the trace remains; history is now trying to define within the documentary material itself unities, totalities, series, relations. History must be detached from the image that satisfied it for so long, and through which it found its anthropological justification: that of an age-old collective consciousness that made use of material documents to refresh its memory; history is the work expended on material documentation (books, texts, accounts, registers, acts, buildings, institutions, laws, techniques, objects, customs, etc.) that exists, in every time and place, in every society, either in a spontaneous or in a consciously organised form. The document is not the fortunate tool of a history that is primarily and fundamentally memory; history is one way in which a society recognises and develops a mass of documentation with which it is inextricably linked.
To be brief, then, let us say that history, in its traditional form, undertook to ‘memorise’ the monuments of the past, transform them into documents, and lend speech to those traces which, in themselves, are often not verbal, or which say in silence something other than what they actually say; in our time, history is that which transforms documents into monuments. In that area where, in the past, history deciphered the traces left by men, it now deploys a mass of elements that have to be grouped, made relevant, placed in relation to one another to form totalities. There was a time when archaeology, as a discipline devoted to silent monuments, inert traces, objects without context, and things left by the past, aspired to the condition of history, and attained meaning only through the restitution of a historical discourse; it might be said, to play on words a little, that in our time history aspires to the condition of archaeology, to the intrinsic description of the monument.
This has several consequences. First of all, there is the surface effect already mentioned: the proliferation of discontinuities in the history of ideas, and the emergence of long periods in history proper. in fact, in its traditional form, history proper was concerned to define relations (of simple causality, of circular determination, of antagonism, of expression) between facts or dated events: the series being known, it was simply a question of defining the position of each element in relation to the other elements in the series. The problem now is to constitute series: to define the elements proper to each series, to fix its boundaries, to reveal its own specific type of relations, to formulate its laws, and, beyond this, to describe the relations between different series, thus constituting series of series, or ‘tables’: hence the ever-increasing number of strata, and the need to distinguish them, the specificity of their time and chronologies; hence the need to distinguish not only important events (with a long chain of consequences) and less important ones, but types of events at quite different levels (some very brief, others of average duration, like the development of a particular technique, or a scarcity of money, and others of a long-term nature, like a demographic equilibrium or the gradual adjustment of an economy to climatic change); hence the possibility of revealing series with widely spaced intervals formed by rare or repetitive events. The appearance of long periods in the history of today is not a return to the philosophers of history, to the great ages of the world, or to the periodisation dictated by the rise and fall of civilisations; it is the effect of the methodologically concerted development of series. In the history of ideas, of thought and of the sciences, the same mutation has brought about the opposite effect; it has broken up the long series formed by the progress of consciousness, or the teleology of reason, or the evolution of human thought; it has questioned the themes of convergence and culmination; it has doubted the possibility of creating totalities. It has led to the individualisation of different series, which are juxtaposed to one another, follow one another, overlap and intersect, without one being able to reduce them to a linear schema. Thus, in place of the continuous chronology of reason, which was invariably traced back to some inaccessible origin, there have appeared scales that are sometimes very brief, distinct from one another, irreducible to a single law, scales that bear a type of history peculiar to each one, and which cannot be reduced to the general model of a consciousness that acquires, progresses, and remembers.
- Source:The Archaeology of Knowledge (1969), publ. Routledge, 1972. Excerpt from the first 3 chapters of main body of work.
theory of forms
LM: I think I disagree with the extended notion that the “forms” exist seperate to ourselves and are an innate aspect of reality. To me, this idea of objective truth seems flawed because, when representated via semantics, it seems to be a subjective interpretive experience. The notion of studying the “building blocks” of language and how it functions as an iconographical code of signifiers, however, seems very useful. Indeed it is the foundation of how we communicate and translate meaning.
In terms of the poetry of understanding, although I may not fully accept Plato’s theory, the thought that “forms” are forgotten memories being relearned or remembered is interesting. I find it difficult to accept because there is no scientific foundation upon which to situate this logic, however there is something compelling in proposing a link between ideas and collective memory. To me, it brings to mind thoughts of dreams and how they might relate to the human experience.
Art Documentaries
Via ABC iview
Born to Fly: Elizabeth Streb Vs Gravity
In an introduction to Streb’s life and work that peaks with a series of breathtaking performances at the London Olympics, seasoned documentarian Catherine Gund constructs a layered evolutionary portrait of an artist.
http://iview.abc.net.au/programs/born-to-fly-elizabeth-streb-vs-gravity/ZW0370A001S00
LM : Amazing amazing imagery. Incredible to see human bodies using simple augmentation, gravity & movement to create mind bending, beautiful works of art.
The dancers, although sometimes seriously injured in the process of actualising Elizabeth Streb’s practice, refer to a “magic” which exists in the world of this art form – creating an impression of “anything is possible”.
Patricia Piccinini: A Dark Fairytale
A portrait of world-renowned Australian artist Patricia Piccinini, famous for her bizarre creatures. See a pivotal moment of change as she creates a new body of work that includes Skywhale – a massive hot-air-balloon.
http://iview.abc.net.au/programs/patricia-piccinini-a-dark-fairytale/AC1247V001S00
When Bjork Met Attenborough
Award-winning musician Bjork and legendary broadcaster and naturalist David Attenborough tell the remarkable story of how and why music has evolved and explore our unique relationship with music.
http://iview.abc.net.au/programs/when-bjork-met-attenborough/ZX9756A001S00
LM : Illustrates the use of the patterns and formulas of nature within music by Bjork. Crystals of different geometry inspire different time signatures.
Bjork: “…4/4, which is like a square”
Attenborough: “Or in this case a cube”
Bjork: “yes”
Frei Otto
Around the beginning of the 1990s, Frei Otto and his team at the Institute for Lightweight Structures in Stuttgart studied what they called “optimized path systems.” Previously, similar to the chain modeling technique Gaudí used for the Sagrada Familia, they had experimented with material systems for calculating form. Each of these material machines was devised so that, through numerous interactions among its elements over a certain time span, the machine restruc- tures, or as Frei Otto says, “finds (a) form.” Most of them consist of materials that process forces by transformation, which is a special form of analog com- puting. Since the materials function as “agents,” it is essential that they have a certain flexibility, a certain amount of freedom to act. It is also essential howev- er, that this freedom is limited to a certain degree set by the structure of the machine itself.
…
The material interactions frequently result in a geometry that is based on complex material behaviour of elasticity and variability. Sand, balloons, paper, soap film (including the famous minimal surfaces for the Munich Olympic Stadium), soap bubbles, glue, varnish, and the ones I will be referring to here: the wool-thread machines. This last tech- nique was used to calculate the shape of two-dimensional city patterns, but also of three-dimensional cancellous bone structure or branching column systems. They are all similar vectorized systems that economize on the number of paths, meaning they share a geometry of merging and bifurcating.
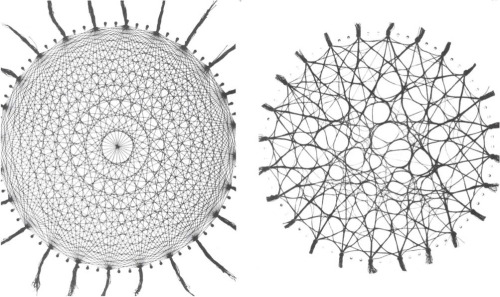
Wool Thread Experiments | Frei Otto + The Institute for Lightweight Structures
Video: Frei Otto Experimenting with Soap Bubbles
15 March, 2015 by José Tomás Franco
Translated by Katie Watkins
“The computer can only calculate what is already conceptually inside of it; you can only find what you look for in computers. Nevertheless, you can find what you haven’t searched for with free experimentation.” – From A Conversation with Frei Otto, by Juan Maria Songel
For Frei Otto, experimentation with models and maquettes was a fundamental part of his work as an architect. In 1961, he began to conduct a series of experiments with soap bubbles (featured in the video above). His experiments centered on suspending soap film and dropping a looped string into it to form a perfect circle. By then trying to pull the string out a minimal surface was created. It was these created surfaces that Otto experimented with.
Through these types of experimentation he was able to build forms and structures that were previously believed to be impossible. “Now it can be calculated, but for more than 40 years it was impossible to calculate it. I have not waited for it to be calculated in order to build it.”
Skeletons, Soap Bubbles and Spider Webs
Insight, 27. March 2015
…After the rigid, weighty formalism of the Third Reich, post-war architecture in West Germany strove above all for lightness and openness, transparency and elegance. More than any other German architect, Frei Otto embodies this endeavor to create lightweight structures that, being derived from nature, make efficient use of materials – designs that are both stunningly beautiful and functional. His work was soon given labels such as “organic”, “Gothic” and “democratic.”
His first name, Frei, which also means “free,” matched his thinking. For him, an architect was simultaneously an explorer, an inventor, an engineer, a humanist and, above all, an interdisciplinary team-worker. Otto’s designs are all the product of collaboration. He worked with Rob Krier, Günther Behnisch, Christoph Ingenhoven and Shigeru Ban – some of the most interesting architects of the twentieth century. It says a lot for Otto that he engaged with the work of such very different architects and cooperated with them so successfully. He referred to himself as a “source of ideas” who “has built little and instead devises ‘castles in the air’” – an understatement if ever there was one.
…His designs, which followed the principle of “do more with less,” were simultaneously experimental, original and unprecedented. Otto’s sophisticated and almost sculptural lightweight structures, using cable nets, lattice shells, or other tensile constructions, made him one of the most important architects and engineers of the twentieth century. His thinking harmonized structural engineering with spatial composition in a way equaled only by Richard Buckminster Fuller in the 1960s and Santiago Calatrava today. Frei Otto was mostly inspired by natural phenomena such as skeletons, spider webs and bubbles – his works express both lightness and stability, fusing architecture with landscape, wall with ceiling, and interior with exterior.
German Pavilion at Expo 67 in Montreal (Photo: Burkhardt)
Working model of light scoops for the main station Stuttgart (Photo: saai)
MINIMAL STRUCTURAL SYSTEM
By This model uses the process I have previously explored, of minimal path systems by Frei Otto, but attempts to take the concept a stage further to create a minimal structural system.
Le Ricolais
1894-1977
Le Ricolais was considered along with Fuller & Otto a leading expert on structural morphology in architecture. He was an engineer, architect, poet and painter, known for his theoretical research on trellis structures and tensegrity during the 1950’s. His work’s roots are in nature and science, in a seashell, a soap bubble or le Ricolais’ fantasy of ‘going inside a rope’ to find a new way to realize his central vision of zero weight, infinite span.
In 1935, as a practicing hydraulics engineer, he introduced the concept of corrugated stress skins to the building industry and was awarded the Medal of the French Society of Civil Engineers. Then in 1940 his work on three-dimensional network systems introduced many architects to the concept of ‘space frames.’ After years of research he was well established as the ‘father of space structures.’
Le Ricolais quote : ‘the art of structure is where to put the holes.’
PARAMETRIC SEMIOLOGY
Harvard GSD | Fall 2013 | Studio Patrik Schumacher & Marc Fornes
Category Archives: Grp04_WoolThreads
Fall 2013 | GSD Studio-project : Patrik Schumacher & Marc Fornes
Parametric Semiology – High Performance Architecture for Apple, Google and Facebook
Abstract:
All problems of society are problems of communication. Especially within post-Fordist network society, total social productivity increases with the density of communication. High performance organisations are thus marked out by a high density/intensity of communication. The life process of society is a communication process that is structured by a rich, diversified panoply of institutions and communicative situations. It is the built environment that stabilizes this matrix of institutions and makes it navigable. The built environment is society’s physical memory; it functions as a system of signification that we all intuitively navigate to find relevant communication partners or situations. The societal function of urban and architectural design is the innovative ordering and framing of communicative interaction. The architectural frames – the designed settings/spaces – are themselves communications: they are communications that define, premise and prime the communicative interactions that are expected to take place within the respectively framed territory. Each territory/frame is embedded within a system of frames that can be understood and designed as a system of signification.
Every talented/successful designer adapts to and intervenes intuitively within the spontaneous and historically evolving semiological system of the built environment. The aim of the project brief is it to move from an intuitive participation within an evolving semiosis to an explicit design agenda that understands the design of a large scale architectural complex – like a corporate campus – as an opportunity to design a new, coherent spatio-morphological system of signification. High performance, creative organisation like Apple, Google or Facebook are the perfect clients for a design approach that aspires to become a global best practice for 21st century architecture. Organisation like Apple, Google or Facebook entail a sufficiently large and complex matrix of social institutions and specific communicative situations, so as to warrant and enable the design of a rich architectural language. The designed Apple campus, Google campus or Facebook campus should be an information-rich, densely articulated environment that orders and encodes the manifold social interactions to be expected and thus facilitates orientation and communication.
The designed semiological system should be conceived as a parametric system, i.e. the various distinctions and their correlations are subject to parametric variation. The programme domain, the domain of the signified, is best understood in terms of interaction patterns or communicative activities. These patterns of communicative interaction can be modelled via programmed agents that respond to the coded environmental clues. This implies that the meaning of architecture can enter the digital model (design medium) and thus becomes the object of cumulative design elaboration. The system of signification works if the agents consistently respond to the relevant positional and morphological clues so that behaviours to be expected can be read off the articulated environmental configuration. As agents cross significant thresholds their behavioural rules are modulated. Territorial distinctions thus order and coordinate interaction patterns. The meaning of architecture, the prospective life processes it frames and sustains, can be modelled and assessed within the design process, thus becoming a direct object of creative speculation.
Tensile Fabric Architecture: An Overview
A great set of 4 mini-documentaries about Tensile Structures, very complete and informative.
Interested in knowing more about tensile fabric structures and the technology behind them? From yurts made out of animal skins to modern and even futuristic building schemes, this video series shows just how exciting and inspiring tensile membranes can be. Divided into four bite size videos, this series covers: Part One: The Materials & Forms of Fabric Architecture Part Two: The Benefits of Fabric Architecture Part Three: The Practicalities of Fabric Architecture Part Four: The Process of Fabric Architecture
You can find them here:
See also : http://fabricarchitecturemag.com/
Marsyas installation at the Tate Modern by Anish Kapoor
Art work by Jens J. Meyer
Flexible matter
Design experiments with analogue and digital form-finding of tensile structures
Lecturer: Ioanna Symeonidou, Dipl. Eng. MSc AA EmTech
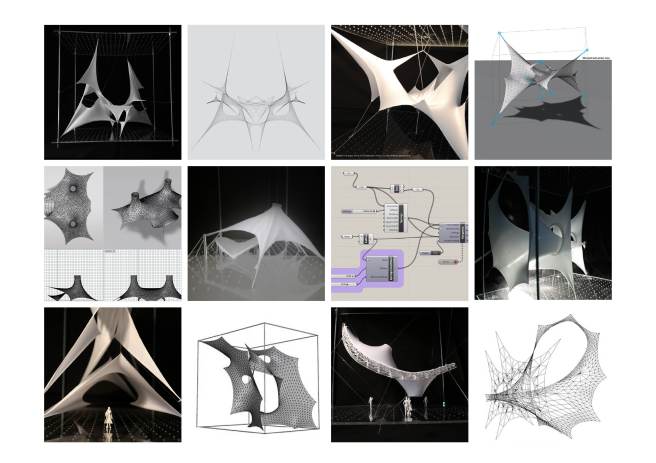
The workshop will explore lightweight structures through the use of mixed media, like analogue form-finding models with membranes and elastic textiles, as well as digital simulations, mainly dynamic relaxation in Rhino.
This intensive hands-on approach will familiarize students with physical simulations, and more specifically spring-particle systems. Digital experiments will be carried out in Rhino, using Grasshopper and Kangaroo plugin, a specifically architectural physics engine.
“To work with a minimal amount of materials using a minimum of energy, this can lead to a new architecture of lightness.”
— Frei Otto
Gaudi
I first ran into Gaudi’s work in Barcelona about 7 years ago, literally on the street. I missed the cathedral but I remember roaming around the city and seeing some unique, unusual buildings. The striking aesthetic created vivid memories, and maybe subconsciously coloured the texture & experience of the city. It was unlike anything I’d seen. It was awesome.
Casa Batlló, Barcelona, Attribution: Rapomon
| Alternative names | Casa dels ossos (House of Bones) |
|---|
Recently I’ve been researching architecture & it’s cross-overs with art, studying designers who work in a space between creativity, engineering and function. I found this;
Emergent Explorations: Analog and Digital Scripting
Master of Architecture thesis paper by Alexander Worden
Abstract
This book documents an exploration of emergent and linear modes of defining space, form, and structure. The thesis highlights a dialog between analog and digital modeling techniques, in concept and project development. It identifies that analog modeling techniques, coupled with judgment, can be used to develop complex forms. The thesis project employs critical judgment and the textile techniques of crochet as a vehicle generate form.Crochet lends itself to this investigation because it is a serial process of fabrication that allows for the introduction of specific non-linear modifications. The resulting emergent forms produced by this mode of working can be precisely described by digital modeling techniques. These analog crochet models are translated into the digital through the employment of advanced digital modeling tools. This translation enables the visualization, development, testing, and execution of an architectural space, form, and structure.
Really useful and relevant as Worden critically reflections upon analog design processes and their relationship to digital representations, using crochet as a case study!
But it gets better, the first artistic reference being put forward (I’m skipping over boatbuilding techniques) is Gaudi and his use of string models.
& so began the googling…
Antoni Gaudí
From Wikipedia, the free encyclopedia
Antoni Gaudí i Cornet (Catalan pronunciation: [ənˈtɔni ɣəwˈði]; 25 June 1852 – 10 June 1926) was a Spanish Catalan architect from Reus/Riudoms and the best known practitioner of Catalan Modernism. Gaudí’s works reflect an individualized and distinctive style. Most are located in Barcelona, including his magnum opus, the Sagrada Família.
Under the influence of neo-Gothic art and Oriental techniques, Gaudí became part of the Modernista movement which was reaching its peak in the late 19th and early 20th centuries. His work transcended mainstream Modernisme, culminating in an organic style inspired by natural forms. Gaudí rarely drew detailed plans of his works, instead preferring to create them as three-dimensional scale models and molding the details as he conceived them.
Quest for a new architectural language
Gaudí is usually considered the great master of Catalan Modernism, but his works go beyond any one style or classification. They are imaginative works that find their main inspiration in nature. Gaudí studied organic and anarchic geometric forms of nature thoroughly, searching for a way to give expression to these forms in architecture. Some of his greatest inspirations came from visits to the mountain of Montserrat, the caves of Mallorca, the saltpetre caves in Collbató, the crag of Fra Guerau in the Prades Mountains behind Reus, the Pareis mountain in the north of Mallorca and Sant Miquel del Fai in Bigues i Riells.[59]
Geometrical forms
The nave in the Sagrada Familia with a hyperboloid vault. Inspiration from nature is taken from a tree, as the pillar and branches symbolise trees rising up to the roof.
This study of nature translated into his use of ruled geometrical forms such as the hyperbolic paraboloid, the hyperboloid, the helicoid and the cone, which reflect the forms Gaudí found in nature.[60] Ruled surfaces are forms generated by a straight line known as the generatrix, as it moves over one or several lines known as directrices. Gaudí found abundant examples of them in nature, for instance in rushes, reeds and bones; he used to say that there is no better structure than the trunk of a tree or a human skeleton. These forms are at the same time functional and aesthetic, and Gaudí discovered how to adapt the language of nature to the structural forms of architecture. He used to equate the helicoid form to movement and the hyperboloid to light. Concerning ruled surfaces, he said:
Paraboloids, hyperboloids and helicoids, constantly varying the incidence of the light, are rich in matrices themselves, which make ornamentation and even modelling unnecessary.[61]
Gaudí evolved from plane to spatial geometry, to ruled geometry. These constructional forms are highly suited to the use of cheap materials such as brick. Gaudí frequently used brick laid with mortar in successive layers, as in the traditional Catalan vault, using the brick laid flat instead of on its side.[63] This quest for new structural solutions culminated between 1910 and 1920, when he exploited his research and experience in his masterpiece, the Sagrada Família. Gaudí conceived the interior of the church as if it were a forest, with a set of tree-like columns divided into various branches to support a structure of intertwined hyperboloid vaults. He inclined the columns so they could better resist the perpendicular pressure on their section. He also gave them a double-turn helicoidal shape (right turn and left turn), as in the branches and trunks of trees. This created a structure that is now known as fractal.[64] Together with a modulation of the space that divides it into small, independent and self-supporting modules, it creates a structure that perfectly supports the mechanical traction forces without need for buttresses, as required by the neo-Gothic style.[65] Gaudí thus achieved a rational, structured and perfectly logical solution, creating at the same time a new architectural style that was original, simple, practical and aesthetic.
Surpassing the Gothic
Another of Gaudí’s innovations in the technical realm was the use of a scale model to calculate structures: for the church of the Colònia Güell, he built a 1:10 scale model with a height of 4 metres (13 ft) in a shed next to the building. There, he set up a model that had strings with small bags full of birdshot hanging from them. On a drawing board that was attached to the ceiling he drew the floor of the church, and he hung the strings (for the catenaries) with the birdshot (for the weight) from the supporting points of the building—columns, intersection of walls. These weights produced a catenary curve in both the arches and vaults. At that point, he took a picture that, when inverted, showed the structure for columns and arches that Gaudí was looking for. Gaudí then painted over these photographs with gouache or pastel. The outline of the church defined, he recorded every single detail of the building: architectural, stylistic and decorative.[68]
Gaudí’s position in the history of architecture is that of a creative genius who, inspired by nature, developed a style of his own that attained technical perfection as well as aesthetic value, and bore the mark of his character. Gaudí’s structural innovations were to an extent the result of his journey through various styles, from Doric to Baroque via Gothic, his main inspiration. It could be said that these styles culminated in his work, which reinterpreted and perfected them.
LM: I remember the gothic Architecture as a feature of Barcelona, so it makes sense to me that this landscape might have inspired Gaudi. Part of his genius seems to be the ability to contribute something to the city which pays homage to this history while furthering ideas of what is creatively possible.
Legacy
After his death, Gaudí’s works suffered a period of neglect and were largely unpopular among international critics, who regarded them as baroque and excessively imaginative. In his homeland he was equally disdained by Noucentisme, the new movement which took the place of Modernisme. In 1936, during the Spanish Civil War, Gaudí’s workshop in the Sagrada Família was ransacked and a great number of his documents, plans and scale models were destroyed.
Gaudí’s reputation was beginning to recover by the 1950s, when his work was championed not only by Salvador Dalí but also by architect Josep Lluís Sert. In 1952, the centenary year of the architect’s birth, the Asociación de Amigos de Gaudí (Friends of Gaudí Association) was founded with the aim of disseminating and conserving his legacy. Four years later, a retrospective was organised at the Saló del Tinell in Barcelona, and the Gaudí Chair at the Polytechnic University of Catalonia was created with the purpose of deepening the study of the Gaudí’s works and participating in their conservation. These events were followed in 1957 by Gaudí’s first international exhibition, held at the Museum of Modern Art in New York City. In 1976, on the 50th anniversary of his death, the Spanish Ministry of Foreign Affairs organised an exhibition about Gaudí and his works that toured the globe.[148]
Between 1950 and 1960, research and writings by international critics like George R. Collins, Nikolaus Pevsner and Roberto Pane spread a renewed awareness of Gaudí’s work, while in his homeland it was admired and promoted by Alexandre Cirici, Juan Eduardo Cirlot and Oriol Bohigas. Gaudí’s work has since gained widespread international appreciation, such as in Japan where notable studies have been published by Kenji Imai and Tokutoshi Torii. International recognition of Gaudí’s contributions to the field of architecture and design culminated in the 1984 listing of Gaudí’s key works as UNESCO World Heritage Sites.[149] Gaudí’s style have subsequently influenced contemporary architects such as Santiago Calatrava[150] and Norman Foster.[151]
Due to Gaudí’s profoundly religious and ascetic lifestyle, the archbishop of Barcelona, Ricard Maria Carles proposed Gaudí’s beatification in 1998. His beatification was approved by the Vatican in 2000.[152] In 1999, American composer Christopher Rouse wrote the guitar concerto Concert de Gaudí, which was inspired by Gaudí’s work; it went on to win the 2002 Grammy Award for Best Classical Contemporary Composition.[153]
The Geometry of Antoni Gaudi
Antoni Gaudi i Cornet (1852-1926) was a well-known architect from Spain. He was born in 1852 as the son of a copper-smith. He studied architecture in Barcelona and combined an interest in history, mathematics and nature to create a rather unique style.
Tesselations
Detail of pillar at the Parc Guell.
Wall at the Parc Guell.
Gaudi used mosaics in many of his works and he created several tiled floors and ceilings in the houses and parks he designed. The mosaics used in Gaudi’s work are an example of Catalan modernism and are sometimes referred to as trencadís.
There are several true periodic tessellations. Many of them are based on the square, but there are also a couple of tessellations based on the hexagon and a wood inlay with a pattern consisting of triangles.
 |
 |
 |
| A tessellation based on squares. | Another tessellation based on squares, | A hexagonal tessellation, but only 3-fold symmetry. |
 |
 |
 |
| Tessellation and optical illusion | Triangular tessellation | Another tiling |
Catenary Arches and Catenoids
A catenary arch is the shape one gets when we suspend a rope or chain from its endpoints. Gaudi used catenary arches in many of his projects. The advantage of the catenary arch is that it can be constructed from relatively light materials while still being able to support great weights.
In La Pedrera (also known as Casa Milà) a model of suspended chains is on view. A mirror below the model shows the reflected image of the structures.
 |
 |
| Suspended chains form catenoids | The reflection shows at outline of arched buildings |
The design of the Church at Santa Coloma de Cervello.
Ruled Surfaces
Ruled surfaces are created by sweeping a line through space.[2] A simple example of a ruled surface is the cylinder one gets if we connect all the points in one circle with their corresponding point on another circle (see image below in the hyperboloid of one sheet section). Gaudi used several of these ruled surfaces in his designs.
Hyperboloids of One Sheet
A hyperboloid can be created if a column of strings is twisted about its central axis. Gaudi used this type of curved surface in the construction of some of the windows in the Sagrada Família in Barcelona.
The cloister walls have window created from 10 hyperboloid sheets which are arranged in a hexagonal honeycomb pattern.
 |
 |
 |
| Twisting a cylinder gives a hyperboloid. | Model of Hyperboloid | Cloister wall, Sagrada Familia. |
Hyperbolic Paraboloids
The hyperbolic paraboloid looks somewhat like a saddle. A simple formula for such a surface is z = x y. [3]
 |
 |
 |
| Model of hyperbolic paraboloid from the Museum at the Sagrada Familia | Computer generated model | Arch by Gaudi |
Some of the cross sections of the hyperbolic paraboloids are parabolas. This can be used to create parabolic arches.
Image by memetician
Gaudí’s hanging chain models: parametric design avant la lettre?
By Rafael Gomez-Moriana / 2012/08/16
Funicular chain model of Colonia Güell church project by Antoni Gaudí, as exhibited at Colonia Güell Interpretive Centre.
Only the crypt was realized.
Interior view of Colonia Güell Crypt
It is known that Gaudí hated drawing and preferred to use models as design tools; especially ones made of chains hung from a ceiling, or strings with small weights attached. Through experimentation with such models, he discovered a way to use traditional Catalan masonry techniques in new, more complex ways. A chain suspended simply from both its ends results in a catenary curve that naturally distributes the static load — in this case tension — evenly between the links of the chain. When this shape is flipped vertically and the materials become brick or stone, then the static load — now compressive — is similarly evenly distributed, resulting in an optimally efficient arch. This was already known for centuries. What Gaudí did was to apply this tension-compression analogy to chains hanging from chains (or arches superimposed on arches) asymmetrically, permitting him to design a much more fluid architecture.
Gaudí made the models of his buildings upside-down, then, using mirrors on the floor, visualized his designs downside-up. He also took photographs of these “wire-frame” models of sorts and “filled” them in with color to generate “solid model renderings”, so to speak. All this has been well-documented in publications and exhibitions.
What is interesting is how, in the process, Gaudí effectively invented a kind of “parametric” design process long before the invention of the computer (let alone the development of software such as Maya or the Grasshopper plug-in for Rhino). One feature of so-called parametric design software is that it updates a complete three-dimensional digital model of a building every time any parameters are altered, allowing alternatives to be studied and compared in the search for a design that performs optimally (although to many architects who use this software it seems that the most important parameter is aesthetic form). Gaudí’s hanging chains do exactly that: if a chain end-point is moved so as to enlarge or reduce, say, the floor plan in one corner, then the shape of the entire hanging chain model shifts and settles into a newly optimized catenary geometry. Of course, parametric design software does a great deal more, but at their conceptual root both of these modeling tools — one physical and the other digital — are analogous.
Catenary
From Wikipedia, the free encyclopedia
In physics and geometry, a catenary[p] is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends. The curve has a U-like shape, superficially similar in appearance to a parabola, but it is not a parabola: it is a (scaled, rotated) graph of the hyperbolic cosine. The curve appears in the design of certain types of arches and as a cross section of the catenoid—the shape assumed by a soap film bounded by two parallel circular rings.
The catenary is also called the alysoid, chainette,[1] or, particularly in the material sciences, funicular.[2]
History
Antoni Gaudí‘s catenary model at Casa Milà
The word catenary is derived from the Latin word catena, which means “chain“. The English word catenary is usually attributed to Thomas Jefferson,[3][4] who wrote in a letter to Thomas Paine on the construction of an arch for a bridge:
I have lately received from Italy a treatise on the equilibrium of arches, by the Abbé Mascheroni. It appears to be a very scientifical work. I have not yet had time to engage in it; but I find that the conclusions of his demonstrations are, that every part of the catenary is in perfect equilibrium.
— [5]
Further Reading:
PDF] Validating Thrust Network Analysis using 3D-printed, structural models
P Block, L Lachauer, M Rippmann – Proceedings of the …, 2010 – block.arch.ethz.ch
… An example of a similar challenge is the translation of the hanging string model
for the crypt of the Colonia Güell Church into an actual stone structure. It is Antoni
Gaudí who was able to see form through these strings. …
for the crypt of the Colonia Güell Church into an actual stone structure. It is Antoni
Gaudí who was able to see form through these strings. …
[PDF]Topological method of construction of point surfaces as physical models
D Kozlov – cumincad.architexturez.net
…Gaudi approximated the catenary with parabolic arches in his early structures, but lately he made several spatial suspended stringmodels for his churches. When the models were inverted, the polygons formed by the strings yielded the directions of the supports. …
Confidence, tolerance, and allowance in biological engineering: The nuts and bolts of living things
… calculations is provided by the techniques developed by the Spanish architect Antoni Gaudí (1852–1926 … By creating an upside-down image of such a string-weight model, the arches and … components in a difficult assembly, so that nature itself (ie gravity in Gaudi’s case) provides …
[PDF]The Square Cube Law: From Vitruvius to Gaudi
JL González – Razones Gaudi, 2002 – arct.cam.ac.uk
… 170-80, http://www.razones-cripta-gaudi.com). … The specific shapes of the elements, structural or not, were based on another of Gaudí’s great innovations: ruled … Sagrada Familia was the direct consequence of the experience at the Güell Colony, although the stringmodel was replaced …
Antoni Gaudí and Frei Otto: Essential Precursors to the Parametricism Manifesto
M Burry – Architectural Design, 2016 – Wiley Online Library
… paraboloid was the obvious solution for four conjoined nonplanar straight edges emerging from the string network that formed the flexible hanging model. bottom: Gaudí used naturally occurring hexagonal basalt prisms from Northern Catalunya for the principal columns. …
Physical modelling and form finding
B Addis – Shell Structures for Architecture: Form Finding and …, 2014 – books.google.com
… engineer Heinrich Hübsch (1795–1863) also used Hooke’s technique, making hanging-string models to determine … who used both two-and three-dimensional hanging models made with strings and bags of … Gaudí used the results of his model tests to complement his use of both …
VIA Page 8 of Emergent Explorations: Analog and Digital Scripting by Alexander Worden;
“Frei Otto and his team from the Institute for Lightweight Structures dedicated an entire IL publication (IL 34: The model) to the reconstruction of Gaudi’s model. Using what little documentation still existed of Gaudi’s original, the IL team was successful in reconstructing the model. Though rebuilding Gaudi’s model occurred in 1982, Otto and his team were exploring natural systems and modeling techniques decades prior to the model. Frei Otto and his team, at the Institute for Lightweight Structures, continued to explore a vast array of different analog machines and natural systems beyond that of the hanging model. Through experiment in techniques and the use of other materials, they continued their search to find form.”
“Emergence is the spontaneous occurrence of an organization or a behavior that is greater than the sum of its parts. – emergence is a change in kind, it is unknown and resembles nothing that we can already see.” (Rahim, 03-80, Catalytic Formations)
Sketches Of Frank Gehry
http://iview.abc.net.au/programs/sketches-of-frank-gehry/ZW0560A001S00
“Who is Frank Gehry, and what makes the rule-breaking architect tick? That’s what filmmaker — and friend of Gehry — Sydney Pollack aims to find out in this documentary.
This program was published 21 hours ago and is available until 2:00am on 2 May 2016. ”
Algorythms
Are Algorythms Conceptual Art’s Next Frontier?
Nicholas o’brien
March 24, 2015, 1:22pm
“Are algorithms art? What happens to the intellectual property at the point of sale? What is actually acquired when one purchases an algorithm? Who would even buy an algorithm?
When I discussed some of these initial questions with Sebastian Chan from The Smithsonian’s Cooper Hewitt Museum, he said, “It’s interesting what happens to things that aren’t able to be contained as a physical thing. We should consider them in another way and we should try to look at what their role is.”
….
However, Artsy engineer Daniel Doubrovkine commented that contemporary museums and institutions are still struggling to present code-based works in the same faithful fashion as conceptual art projects: “I think we need to put code in social context. For example, early programmers were mostly women, and creating exhibitions around women programmers and the art of their programming is a needed social context.”
…
A structural problem with algorithms is that they render the underrepresented into the invisible. If such a process is applied to culture, anything that falls outside the scope of an algorithm is viewed as an anomaly. As a result of the crunching and sorting of data, the process of culture becomes the product of an algorithm. Algorithms are “results- based,” designed objects—machines that use parsing in order to create significance, relevance, and meaning. Algorithms produce evidence to substantiate speculations of all types: financial, informational, social, ideological. What becomes truly troubling is not when statistical aberrations are left out of the mix, but when the results of algorithms create or substantiate a narrative of exclusivity.
…
Unfortunately, the narrative of contemporary algorithmic culture is one that is dominated by particular voices—mostly male, mostly white, and mostly from classes of some privilege. It is not that other voices within the development of code-based works don’t exist, but rather that these voices go unrecognized as a result of being filtered out through algorithmic processes. Although many initiatives are currently undoing and combating exclusion and under-representation, it becomes increasingly difficult to do so when the algorithms we use (and are impacted by) are built upon parameters that disavow the existence of populations that defy categorization or exist contrary to a privileged narrative.
Google Scholar
Search term ‘Crochet’, anywhere in the article, 1995-2016 – 1st page of results shows mostly authors with this name.
Search term ‘Crochet’, in the title of the article, 1995-2016, not including patients – results from 1st page as follows;
[HTML]Ureteral stent retrieval using the crochet hook technique in females
T Kawahara, H Ito, H Terao, T Yamagishi, T Ogawa… – PloS one, 2012 – journals.plos.org
Ureteral stent exchange under fluoroscopic guidance using the crochet hook technique in women
T Kawahara, H Ito, H Terao, Y Yamashita… – Urologia …, 2012 – karger.com
[CITATION] Yarn bombing: The art of crochet and knit graffiti
M Moore, L Prain – 2009 – Arsenal Pulp Press
Nickel allergy in patch‐tested female hairdressers and assessment of nickel release from hairdressers’ scissors and crochet hooks
JP Thyssen, K Milting, A Bregnhøj, H Søsted… – Contact …, 2009 – Wiley Online Library
The 42nd crochet: Getting students hooked into a literacy community
M Boyd, S Kneller – The Reading Teacher, 2009 – Wiley Online Library
Geoeffectiveness of solar flares in magnetic crochet (sfe) production: I—Dependence on their spectral nature and position on the solar disk
JJ Curto, LR Gaya-Piqué – Journal of Atmospheric and Solar-Terrestrial …, 2009 – Elsevier
[BOOK] Stitch’n bitch crochet: The happy hooker
D Stoller – 2006 – books.google.com
[CITATION] Irish Crochet Lace: Motifs from County Monaghan
E d’Arcy – 2003 – Colin Smythe
The crochet hook method of stab avulsion phlebectomy for varicose veins
BE Waddell, MB Harkins, PA Lepage… – The American journal of …, 1996 – Elsevier
[CITATION]Crochet: History & Technique
L Paludan – 1995 – Interweave Press
Search term ‘Crochet semiotic’, anywhere in the article, not including patients – results from 1st page as follows;
Hometown ideology and retailer legitimation: the institutional semiotics of Wal-Mart flyers
SJ Arnold, RV Kozinets, JM Handelman – Journal of Retailing, 2001 – Elsevier
… Next is the heart of the paper—a semiotic analysis of the Wal-Mart flyer … When this semiotically
derived question is posed, the Wal-Mart flyer reveals a considerable amount about the audience …
can help pick each other up just like a family member would do.” The crochet thread is …
derived question is posed, the Wal-Mart flyer reveals a considerable amount about the audience …
can help pick each other up just like a family member would do.” The crochet thread is …
[CITATION] Towards a Semiotic Analysis of Incarceration, Entrapment and Creativity among Women
JA Gibbons
H Sowden – 2015 – wesscholar.wesleyan.edu
… sweaters, slippers, and hats became feasible (Paludan 1995). The most well-known crocheted
item today, the often many-colored or patch- … transforming leftover yarn into something useful,
and in the 1940s crocheting… By the mid-20th century, crochet had firmly exited the …
item today, the often many-colored or patch- … transforming leftover yarn into something useful,
and in the 1940s crocheting… By the mid-20th century, crochet had firmly exited the …
Publication Date
April 2015
Major
Art Studio, Anthropology
Language
English (United States)
Abstract
Definitions of craft abound and the way that craft production is delineated from non-craft production at different historical moments highlights changing views on the sometimes-strict and sometimes-blurry dichotomies between the useful and the decorative, art and craft, mind and body, masculine and feminine. This essay explores discourses surrounding craft production beginning in the European Middle Ages and concluding in present day online craft communities. Crochet, an understudied and under-theorized craft form, is used as a case study to highlight the ways in which contemporary craft practices draw upon shifting historical definitions of craft and self-creation, weaving together a tangled history in the elaboration of every craft object and craft-person.
Correction sequences and semiotic resources in ensemble music workshops: the case of Conduction®
D Veronesi – Social Semiotics, 2014 – Taylor & Francis
… Special Issue: Doing (things with) sounds: Music as a site of social semiosis. … developed so as
to take into account participants’ use of further vocal and visible semiotic resources (prosody,
gestures … [CrossRef], [Web of Science ®] View all references) or to crochet chain stitches …
to take into account participants’ use of further vocal and visible semiotic resources (prosody,
gestures … [CrossRef], [Web of Science ®] View all references) or to crochet chain stitches …
Abstract
The paper examines the phenomenon of correction of musical action by analysing ensemble music workshops devoted to Conduction®, a way of making music together on the basis of a codified gestural lexicon addressed by a conductor to instrumentalists. In particular, it focuses on correction sequences initiated by the conductor and related to the musical material to be played and discusses the techniques used by the conductor to construct and sequentially organize correction, showing how these are accomplished through the interplay and mutual contextualization of talk and further audible and visible semiotic resources. Based on the fine-grained analysis of two correction sequences, the study stresses the role of multimodality for investigating music and pedagogy from an interactional perspective, while highlighting the peculiarities of Conduction as performative and educational practice.
M Hebron – The Journal of Modern Craft, 2013 – Taylor & Francis
… The Flags owe a clear debt to the semiotic queries posed by the Pictures Generation in the
1970s–80s with works by artists like Victor Burgin or Martha … For her Counterfeit Crochet Project
Syjuco invited participants from around the world to make crocheted versions of …
1970s–80s with works by artists like Victor Burgin or Martha … For her Counterfeit Crochet Project
Syjuco invited participants from around the world to make crocheted versions of …
AM Dreher – 2008 – books.google.com
… The exploration of these ‘statements’ and related matters falls to semiotics” (Colapietro, 1993,
p … generally of cambric, elaborately embroidered or trimmed with embroidery, crochet or lace … Historic
and Semiotic Analysis of Illustrated Vogue Magazine Covers 21 helped American …
p … generally of cambric, elaborately embroidered or trimmed with embroidery, crochet or lace … Historic
and Semiotic Analysis of Illustrated Vogue Magazine Covers 21 helped American …
[PDF]A multimodal social semiotic approach to jewellery design pedagogy
S Salaam – 2012 – open.uct.ac.za
… alternative materials or techniques which include unconventional processes such as crochet,
felting or … Karlsson (2011) who present an in depth social semiotic argument regarding materiality …
the social and contextual interests of the individual into semiotically shaped materials. …
felting or … Karlsson (2011) who present an in depth social semiotic argument regarding materiality …
the social and contextual interests of the individual into semiotically shaped materials. …
[CITATION] Ubu and the Signs of the Theater
M Issacharoff – Pre-Text, Text, Context, Robert L. Mitchell ed.( …
[CITATION] The antimacassar in fact and fiction: how textual
A McEwan – Textiles and Text: Re-establishing the Links …, 2007 – Archetype Publications
[CITATION] The more art, the more science: narrative interpretations of art (and life)
S Goett – Working Papers in Art and Design, 2008
The White Review
[Excerpts from]
GABRIEL OROZCO: COSMIC MATTER AND OTHER LEFTOVERS
March 2011, RYE DAG HOLMBOE
‘TO LIVE,’ WRITES WALTER BENJAMIN, ‘MEANS TO LEAVE TRACES’.
…The paradoxically titled YIELDING STONE (1992), for instance, consists of a black lump of plasticine formed in the weight of the artist’s own body. The work is rolled onto the street where this highly malleable and greasy material absorbs whatever residue it encounters….
…YIELDING STONE does not mark the external world but is inscribed with it. Put differently,the work inhabits the world but is also inhabited by it. And secondly, unlike AUTOMOBILE TIRE PRINT, a ‘happening’ that took place only in the moment of its occasion, YIELDING STONE awaits its future actualisation.
…If the work is nostalgic it is not because it harks back to some idealised past but because it is nostalgic for the future. YIELDING STONE is in a perpetual process of becoming. Even as it sits on the gallery floor, isolated and quiescent, it is weighed down by gravity and absorbs the dust on which it rests. One might also say that it is marked, every moment, by the sensation of time.
The enigmatic materiality of this artwork is echoed in LINTELS (2001). Here sheets of lint – the grey stuff leftover in the filters of drying machines – have been hung on several rows of washing line, as though Orozco was hanging his dirty laundry in public. Beyond this bathos, what is of interest is the transience of the material used. Lint is made of human hair and dust, which is made of dead skin cells, as well as fluff. This is the detritus of quotidian life, the stuff we would rather forget about, infinitesimal traces of our own mortality. When compressed in the filter the material is held together, but only temporarily. Pablo Picasso once wrote that ‘art washes away from the soul the dust of everyday life’. This work, however, will return to dust. The air must be full of it. Like YIELDING STONE, a work conscious of its temporal essence, LINTELS internalises its own impermanence. Construction becomes inseparable from dispersal. The artwork, then, is just a hiatus. Like life.
…
Yet, like the synecdochal nature of the works I have considered so far, the metonymy between spit and life is an odd one and warrants closer attention. In his CRITICAL DICTIONARY, Georges Bataille wrote the following definition of the term ‘Formless’, a definition that seems particularly relevant to a work like FIRST WAS THE SPITTING. Indeed, one wonders whether Orozco had it in mind:
For academics to be content, the universe would have to assume a form. All of philosophy has no other goal: it is a matter of fitting what is there into a formal coat, a mathematical overcoat. On the other hand to assert that the universe resembles nothing else and is only formless comes down to stating that the universe is something like a spider or spit.[2]
In FIRST WAS THE SPITTING the use of graph paper – a ‘mathematical overcoat’, stands in deliberate contrast to the formless accumulation of spit in the centre of the page. This could be interpreted as a re-introduction of the somatic and the aleatory into the hard-edged, mathematical reductivism of minimalism. This in turn could be read more widely as a reaction against the increased rationalisation of life in a ‘totally administered world’, to borrow Theodor W. Adorno’s now famous expression. At the same time, however, the graphite and ink markings which expand like constellations or rhizomes around each of the stains exist in a precarious balance. Sometimes the organic substance seems to dictate the composition. At other times Orozco has drawn over the spit and replaced the graph paper’s rigid lines, ‘fitting what is there into a formal coat’.
This is arguably indicative of attentiveness to the violence of a representational economy. In other words, the awareness that the formless cannot be manifested directly without giving it shape. Once the formless – the non-identical, becomes an object of reflexive consciousness, it loses its subversive quality precisely because it is identified as formless. This, then, is something like the contradictory endeavour that preoccupied many of the Surrealists: the conscious manifestation of unconscious drives.
Except that I believe Orozco is more aware of the paradox of representing the unrepresentable than the Surrealists were. This is not only because his works undermine the possibility of full representation, although this certainly forms part of it. Rather, is it because the artist purposely produces irresolvable tensions. Another example of a work that supports this argument is BLACK KITES (1997), a human skull covered in a strict geometric pattern of black and white rhombi. Like FINGER RULER DRAWING,here the Cartesian plane – the permanent idea, is adapted to the contours of the skull – the transitory substance. The oppositions that inhere in both these works: the organic and the inorganic; the corporeal and the cerebral; the rational and the irrational; the transitory and the timeless; and, in the case of BLACK KITES, drawing and sculpture (Orozco was to describe the work with the words ‘Object made image’[3]), are products of different kinds of articulations that produce as well as negate each other, deliberately subverting simplistic bifurcations. Where exactly is the interface anyway?
…The problem the works ultimately raise, I think, is this: can culture be political, which is to say critical and even subversive, or is it necessarily co-opted and subsumed by the social system of which it is a product?
researchlm 
